Toán 10 hàm số bậc hai là một trong những kiến thức Toán quan trọng ở bậc học trung học phổ thông. Do đó, các em cần nắm vững những nội dung trọng tâm liên quan đến chủ đề này như định nghĩa, cách xét dấu, đồ thị của hàm số bậc hai,… cùng các dạng bài tập thường gặp. Team Marathon Education đã tổng hợp và chia sẻ đến các em những kiến thức này qua bài viết dưới đây. Hy vọng rằng bài viết sẽ có ích cho các em trong quá trình học tập.
>>> Xem thêm: Lý Thuyết Toán 10 Hàm Số: Hàm Số Bậc Nhất Và Hàm Số Bậc Hai
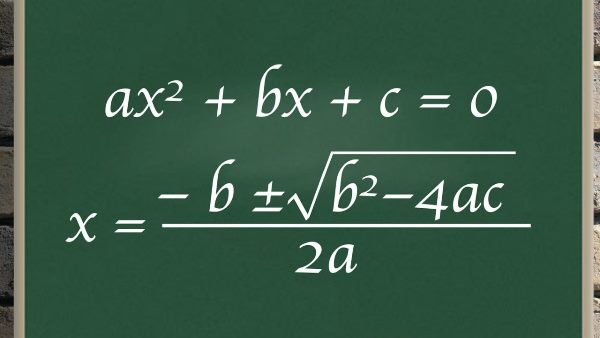
Ta có:
\begin{aligned}
&ax^2+bx+c=a\left(x^2+2\frac{b}{2x}+\frac{b^2}{4a^2}\right)-\frac{b^2}{4a^2}+c\\
&=a\left(x+\frac{b}{2a}\right)^2-\frac{b^2-4ac}{4a}\\
\end{aligned}Nếu ta đặt:
\Delta=b^2-4ac,\ p=-\frac{b}{2a},\ q=-\frac{\Delta}{4a}Hàm số y = ax2 + bx + c (a ≠ 0) sẽ trở thành y = a(x – p)2 + q.
Vì vậy:
\begin{aligned}
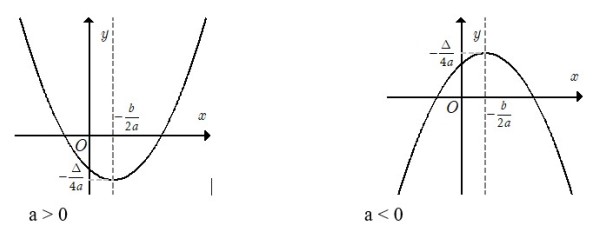
&\footnotesize\text{Đồ thị hàm số bậc hai } y = ax^2 + bx + c \ (a ≠ 0)\text{ là một Parabol có đỉnh }I\left(-\frac{b}{2a};-\frac{\Delta}{4a}\right)\text{nhận đường thẳng}\\
&\footnotesize x=-\frac{b}{2a} \text{ là trục đối xứng và bề lõm hướng lên trên khi a > 0, bề lõm hướng xuống dưới khi a < 0.}
\end{aligned}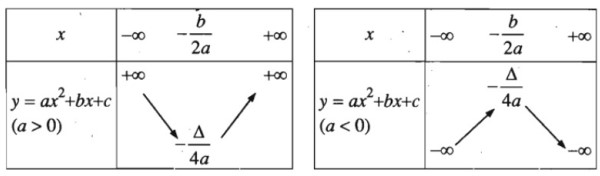
\begin{aligned}
&\footnotesize\bull\text{Khi a dương, hàm số đồng biến trên khoảng }\left(-\frac{b}{2a};+∞\right), \text{ nghịch biến trên khoảng }\left(-∞;-\frac{b}{2a};\right)\text{ và có}\\
&\footnotesize\text{giá trị nhỏ nhất là }-\frac{\Delta}{4a} \text{ khi }x=-\frac{b}{2a}.\\
&\footnotesize\bull\text{Khi a âm, hàm số nghịch biến trên khoảng }\left(-\frac{b}{2a};+∞\right), \text{ đồng biến trên khoảng }\left(-∞;-\frac{b}{2a};\right)\text{ và có}\\
&\footnotesize\text{giá trị lớn nhất là }-\frac{\Delta}{4a} \text{ khi }x=-\frac{b}{2a}.\\
\end{aligned}>>> Xem thêm: Lý Thuyết Toán 10 Dấu Của Tam Thức Bậc Hai Và Cách Xét Dấu
Cách làm
Ví dụ: Xác định Parabol (P) y = ax2 + bx + c (a ≠ 0). Biết rằng (P) đi qua điểm A(2;3) và có đỉnh I(1;2)
Bài giải:
\begin{aligned}
&A ∈ (P) \text{ nên } 3 = 4a + 2b + c\ (1)\\
&(P) \text{ có đỉnh }I(1;2) \text{ nên }-\frac{b}{2a}=1\Leftrightarrow2a+b=0\ (2)\\
&I ∈ (P) \Leftrightarrow 2=a+b+c\ (3)\\
&\text{Từ (1), (2), (3), ta có: } \begin{cases}4a+2b+c=3\\2a+b=0\\a+b+c=2\\
\end{cases}\Leftrightarrow
\begin{cases}a=1\\b=-2\\c=3
\end{cases}\\
&\text{Vậy (P) cần tìm là: }y=x^2-2x+3
\end{aligned}Cách làm
Các bước để vẽ đồ thị hàm số bậc hai y = ax2 + bx + c (a ≠ 0):
\begin{aligned}
&\footnotesize\bull \ \text{Bước 1: Tìm tọa độ đỉnh }I\left(-\frac{b}{2a};-\frac{\Delta}{4a}\right).\\
&\footnotesize\bull \ \text{Bước 2: Tìm trục đối xứng của đồ thị theo công thức }x=-\frac{b}{2a}.\\
&\footnotesize\bull \ \text{Bước 3: Tùy thuộc vào từng hàm số, các em tìm hoành độ và tung độ của các điểm mà đồ thị hàm số bậc }\\
&\footnotesize\text{hai giao nhau với trục hoành và trục tung (nếu có). Ngoài điểm giao nhau, tìm thêm một số điểm đặc biệt của}\\
&\footnotesize\text{đồ thị như điểm đối xứng của các điểm cắt,... giúp đồ thị vẽ một cách chính xác nhất.}\\
&\footnotesize\bull \ \text{Bước 4: Tiến hành vẽ đồ thị theo các điểm đã xác định được.}
\end{aligned}Ví dụ: Vẽ đồ thị hàm số y = x2 + 3x + 2
Bài giải:
Ta có:
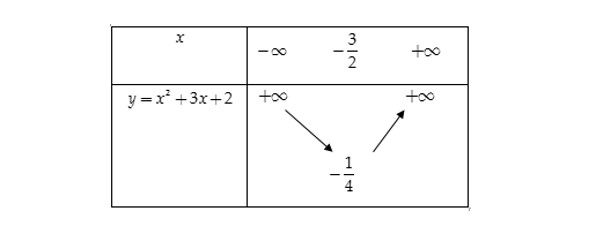
-\frac{b}{2a}=-\frac{3}{2}\ ,\ -\frac{\Delta}{4a}=-\frac{1}{4}Bảng biến thiên:
\begin{aligned}
&\footnotesize\text{Suy ra đồ thị hàm số }y = x^2+3x+2 \text{ có đỉnh là }I\left(-\frac{3}{2};-\frac{1}{4}\right) \text{ và đi qua các điểm A(-2;0), B(-1;0), C(0;2),}\\
&\footnotesize\text{D(-3;2)}.\\
&\footnotesize\text{Đồ thị của hàm số nhận đường thẳng }x=-\frac{3}{2} \text{ làm trục đối xứng và có bề lõm hướng lên trên.}
\end{aligned}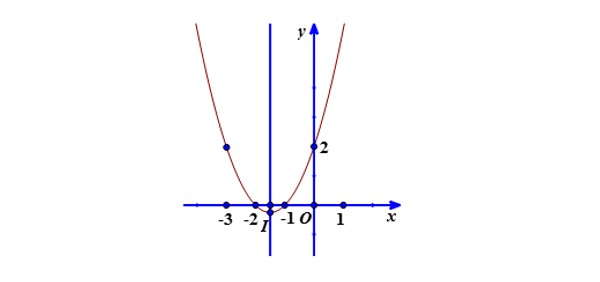
Cách làm
\begin{aligned}
&\footnotesize\text{Dựa theo đồ thị hoặc bảng biến thiên của hàm số } y = ax^2 + bx + c\ (a ≠ 0) \text{các em xác định các điểm max và }\\
&\footnotesize\text{min của hàm số trong khoảng giá trị ⦍a;b⦎ tại }x = a, x = b\text{ hoặc }x=-\frac{b}{2a}.
\end{aligned}Dạng toán này thuộc dạng nâng cao và thường khá ít gặp trong chương trình Toán 10 hàm số bậc hai. Do đó, Marathon chỉ giới thiệu sơ qua về phương pháp giải để các em nắm bắt.
Cách làm
Muốn giải được bài toán tìm tọa độ giao điểm của hai đồ thị f(x) và g(x). Các em giải phương trình hoành độ giao điểm f(x) = g(x) (1)
Ví dụ: Tìm tọa độ giao điểm của đồ thị bậc hai và đường thẳng sau:
(P): y = x2 – 2x – 1 và d: y = x – 1
Bài giải:
Xét phương trình tọa độ giao điểm của (P) và (d):
\begin{aligned}
&\bull x^2 - 4x - 2 = -2x - 2\\
&⇔ 2x^2 - 2x = 0\\
&⇔x= 1 \text{ hoặc } x = 0\\
&\bull x = 0 ⇒ y(0) = 0 - 1 = -1\\
&\bull x = 1 ⇒ y(1) = 1 - 1 = 0\\
&\text{Vậy tọa độ giao điểm cần tìm là }(0;-1) \text{ và }(1;0).
\end{aligned}Để học tốt kiến thức Toán 10 hàm số bậc hai nói riêng hay bộ môn Toán lớp 10 nói chung, ngoài việc học tập chăm chỉ trên lớp các em có thể đăng ký thêm các khóa học online bổ sung kiến thức trực tuyến. Trong đó, Marathon Education là một trong những nền tảng học online livestream cả 3 môn Toán – Lý – Hóa dành cho học sinh trung học phổ thông được nhiều em học sinh tin tưởng lựa chọn.
Khi đến với Marathon, các em sẽ được học tập với đội ngũ giáo viên ưu tú thuộc TOP 1% giáo viên giỏi tại Việt Nam. Ngoài ra, các thầy cô đều có bằng Thạc sĩ trở lên và hơn 10 năm kinh nghiệm giảng dạy. Đặc biệt, với hình thức học livestream, các em có thể tương tác trực tiếp với giáo viên như học trên trường lớp.
Bên cạnh đó, các em sẽ luôn được hỗ trợ tận tình bởi đội ngũ Cố vấn học tập của Marathon. Ngoài ra, khi trở thành học viên, các em còn nhận được sổ tay “siêu xịn” tổng hợp kiến thức Toán – Lý – Hóa. Tài liệu này sẽ hỗ trợ các em ghi nhớ và ôn tập kiến thức dễ dàng hơn.
Marathon Education là nền tảng học online có áp dụng nhiều công nghệ tiên tiến hiện đại. Do đó, chất lượng của các lớp học luôn được đảm bảo với hình ảnh chân thật, âm thanh rõ ràng, đường truyền ổn định và không bị lag,…. Các em sẽ được tạo điều kiện để học tập hiệu quả nhất.
Các em hãy nhanh tay đăng ký các lớp học trực tuyến Toán – Lý – Hóa lớp 10 – 11 – 12 tại Marathon Education trước ngày 15/02/2022 để có cơ hội nhận nhiều ưu đãi lên đến 39% và nhiều phần quà hấp dẫn khác.
Với những thông tin mà Marathon Education đã chia sẻ ở trên, hy vọng các em đã có thể tự mình làm tốt các bài tập về Toán 10 hàm số bậc hai cũng như vẽ đồ thị nhanh chóng. Ngoài việc ghi nhớ các kiến thức trọng tâm, các em hãy thường xuyên làm bài tập. Chúc các em luôn thành công trong các kỳ thi và học tập tốt!