Lũy thừa và hàm số lũy thừa đã không còn xa lạ với chương trình Toán giải tích lớp 12. Kiến thức này thường xuất hiện trong các bài toán về khảo sát hàm số. Team Marathon Education sẽ giúp các em hiểu rõ hơn về khái niệm lũy thừa cũng như đạo hàm của hàm số lũy thừa qua bài viết sau.
>>> Xem thêm: Lý Thuyết Và Đồ Thị Của Hàm Số Mũ, Hàm Số Lôgarit
Các em hãy cùng Marathon tìm hiểu rõ hơn về khái niệm lũy thừa với từng loại số mũ dưới đây.
Định nghĩa: Cho một số nguyên dương n bất kỳ và một số thực a tùy ý. Lũy thừa bậc n của số a là tích của n thừa số a và có dạng
\begin{aligned}
&a^n=a.a.a.....a \ \text{(n thừa số a)}\\
&\text{Với } a \not = 0 \text{ thì } a^0=1, \ a^{-n}=\frac{1}{a^n}
\end{aligned}Lưu ý: 0n và 0-n không có nghĩa.
Tính chất: Lũy thừa với số mũ nguyên sẽ có tính chất tương tự như lũy thừa với số mũ nguyên dương.
\begin{aligned}
&\footnotesize\text{Cho một số thực dương a bất kỳ và r là một số hữu tỉ có dạng }r=\frac{m}{n}\\
&\footnotesize\text{Trong đó m là một số nguyên còn n là một số nguyên lớn hơn 1. Lúc này, }\\
&\footnotesize\text{lũy thừa của a với số mũ r và số }a^r
\footnotesize\text{ xác định bởi:}\\
&a^r=a^\frac{m}{n} =\sqrt[n]{a^m}\\
&\footnotesize\text{Đặc biệt: Khi }m=1\ \text{thì} \ a^\frac{1}{n}=\sqrt[n]{a}
\end{aligned}Cho a, b là những số thực dương và α, β là những số thực dương tùy ý. Khi đó ta có các tính chất của lũy thừa với số mũ thực như sau:
\begin{aligned}
&a^α.a^β=a^{α+β}\\
&\frac{a^α}{a^β}=a^{α-β}\\
&(a^α)^β=a^{αβ}\\
&(ab)^α=a^α.b^α\\
&\left( \frac{a}{b}\right)^α=\frac{a^α}{b^α}\\
& \text{Nếu }a>1\text{ thì } a^α>a^β \Leftrightarrow α>β\\
& \text{Nếu }a<1\text{ thì } a^α>a^β \Leftrightarrow α<β
\end{aligned}Những hàm số có dạng y=xα (α ∈ R) được gọi là hàm số lũy thừa. Tùy thuộc vào α mà mỗi hàm số sẽ có những tập xác định khác nhau:
\begin{aligned}
&\footnotesize\text{Hàm số y}=x^\alpha \text{ có đạo hàm tại mọi }x\in(0;+\infin) \text{ và y'}=(x^\alpha)'=\alpha x^{\alpha-1}.\\
&\footnotesize\text{Nếu hàm số u = u(x) nhận giá trị dương và có đạo hàm trong khoảng J thì }\\
&\footnotesize\text{hàm số } y=u^\alpha(x) \text{ cũng có đạo hàm trên J là:}\\
&y'=[u^\alpha(x)]^{-1}=\alpha x^{\alpha-1}.(x).u'(x)
\end{aligned}Trong trường hợp số mũ nguyên dương, hàm số y = xn có tập xác định R và có đạo hàm trên toàn trục số. Công thức tính đạo hàm hàm số lũy thừa có thể được mở rộng thành:
\begin{aligned}
&\forall x \in \R, \ (x^n)'=nx^{n-1}\\
&\forall x \in J,\ [u^n(x)]'=nu^{n-1} \ (x) \ u'(x) \\
&\text{(nếu u=u(x) có đạo hàm trong khoảng J)}
\end{aligned}Nếu số mũ là số nguyên âm thì hàm số y=xn có tập xác định là R\{0} và có đạo hàm tại mọi x khác 0, công thức đạo hàm hàm số lũy thừa tổng quát được mở rộng thành:
\begin{aligned}
& \forall x \not=0, (x^n)'=nx^{n-1}\\
&\forall x \in J, [u^n(x)]'=nu^{n-1}.(x).u'(x)\\
&\text{(nếu u=u(x) } \not= 0 \text{ có đạo hàm trong khoảng J)}
\end{aligned}\begin{aligned}
&\footnotesize\text{Hàm số }y=\sqrt[n]{x}\text{ có thể được xem như là dạng mở rộng của hàm số lũy thừa }\\
&\footnotesize y=x^\frac{1}{n} \text{ (tập xác định của }y=\sqrt[n]{x}\text{ chứa tập xác định của }y=x^\frac{1}{n} \text{ và trên tập}\\
&\footnotesize\text{xác định của }y=x^\frac{1}{n}\text{thì hai hàm số trùng nhau).}\\
&\footnotesize \text{Công thức tính đạo hàm căn thức:}\\
&\footnotesize y=\sqrt[n]{x}=x^\frac{1}{n} \text{\ \ \ \ và\ \ \ \ } (x^\frac{1}{n})'=\frac{1}{n}x^{\frac{1}{n}-1}\\
&\footnotesize \Rightarrow (\sqrt[n]{x})'=\frac{1}{n\sqrt[n]{x^{n-1}}}\\
&\footnotesize \Rightarrow (\sqrt[n]{u(x)})'=\frac{u'(x)}{n\sqrt[n]{u^{n-1}(x)}}\\
\end{aligned}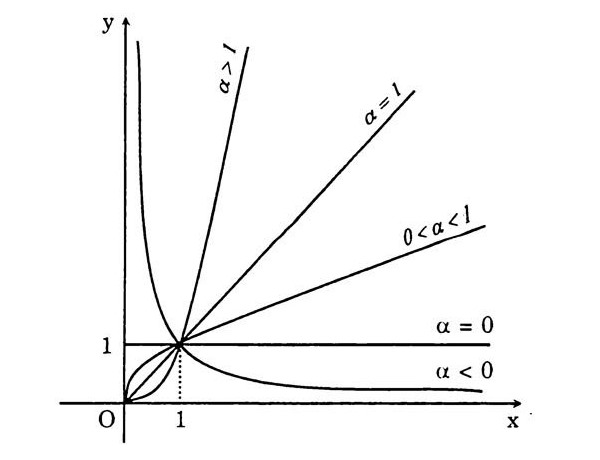
Tính chất của hàm số lũy thừa trên khoảng (0; +∝):
Chú ý: Khi khảo sát hàm số y= xα với α cụ thể thì cần xét hàm số trên toàn bộ tập xác định của nó chứ không phải chỉ xét riêng trên khoảng (0; +∝).
Bên cạnh việc tiếp thu kiến thức trên trường, các em có thể tham gia học livestream cùng Marathon Education để bổ sung thêm kiến thức. Đây là nền tảng các lớp học livestream trực tuyến uy tín dành cho học sinh cấp 3. Marathon Education giảng dạy các môn học thuộc chương trình giáo dục bắt buộc, trong đó có Toán – Lý – Hóa.
Các em sẽ được giảng dạy bởi đội ngũ giảng viên thuộc TOP 1% dạy giỏi tại Việt Nam. Các thầy cô sở hữu bằng cấp từ Thạc sĩ trở lên với hơn 10 năm kinh nghiệm trong ngành.
Marathon Education cũng chú trọng nâng cấp trang thiết bị, ứng dụng thông tin dữ liệu và nền tảng công nghệ mới nhất để đảm bảo không xảy ra tình trạng giật, lag, mất âm thanh hay hình ảnh không rõ trong tiết học.
Hơn thế, thông qua hình thức học livestream, học sinh có thể tương tác nhiều hơn với giáo viên. Đội ngũ cố vấn học tập của Marathon Education luôn theo sát tiến độ mỗi buổi học, đồng thời hỗ trợ giải đáp thắc mắc và giúp các em cá nhân hóa lộ trình học tập của mình.
Khi đăng ký khóa học, các em sẽ nhận được những sổ tay Toán – Lý – Hóa “siêu xịn”. Tài liệu này có thể giúp các em hệ thống và ghi nhớ kiến thức dễ dàng hơn.
Hiện tại, Marathon Education đang có chương trình ưu đãi 39% học phí dành cho tất cả các học viên đăng ký học livestream trực tuyến Toán – Lý – Hóa lớp 10 – 11 – 12 trong thời gian từ nay cho đến ngày 15/02/2022.
Team Marathon Education đã giúp các em hiểu rõ hơn về hàm số lũy thừa cũng như đạo hàm của chúng. Hãy đăng ký ngay khóa học tại Marathon Education và tham gia lớp học ngoài giờ để trau dồi thêm kiến thức Toán – Lý – Hóa!