Ở chương trình Toán đại số lớp 12, kiến thức về nguyên hàm e mũ u và các hàm số đơn giản đóng vai trò trọng điểm trong các kỳ thi. Để tìm hiểu sâu hơn về nội dung này, các em hãy đọc ngay bài viết dưới đây từ Marathon Education.
>>> Xem thêm: Toán 12 Nguyên Hàm – Lý Thuyết Và Một Số Bài Tập Ví Dụ
Ta có: ký hiệu K là đoạn, nửa khoảng hoặc khoảng của tập R.
Cho hàm số f(x) đã được xác định trên K, nếu F’(x) = f(x) với mọi giá trị x ∈ K, ta có thể khẳng định rằng F(x) được gọi là nguyên hàm của hàm số f(x).
Một số định lý về nguyên hàm:
Liên quan đến định nghĩa cũng như định lý về nguyên hàm, các em cũng cần phải ghi nhớ một số tính chất quan trọng như sau:
Trước khi đi vào phần lý thuyết về nguyên hàm e mũ u, các em cần phải nắm chắc một số phần kiến thức trọng tâm về hàm số mũ như sau:
Hàm số mũ được định nghĩa là hàm số ở dạng y = ax với điều kiện hệ số a luôn dương và khác giá trị 1.
Hàm số mũ y = ax (a>0, a1) sẽ tồn tại một số tính chất như sau:
>>> Xem thêm: Lý Thuyết Và Đồ Thị Của Hàm Số Mũ, Hàm Số Lôgarit
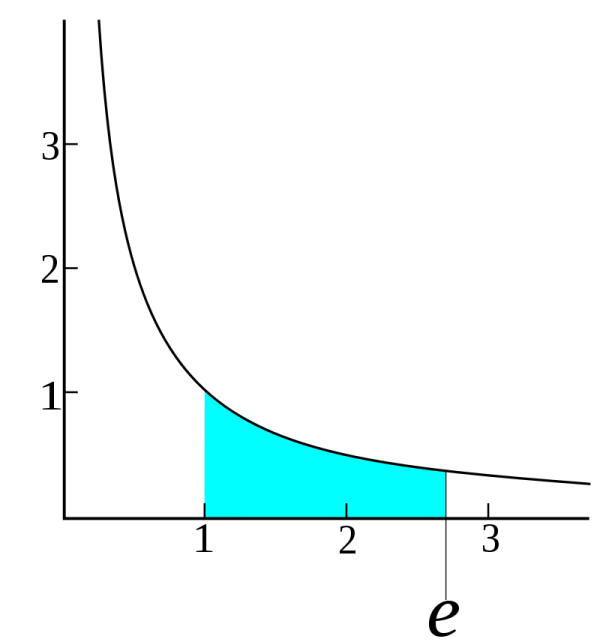
Số e là một hằng số toán học có giá trị gần bằng với 2,71828… Hằng số này có thể được biểu diễn ở nhiều cách khác nhau. Cụ thể:
\begin{aligned}
&\footnotesize\bull\text{Số e là số thực dương duy nhất mà giá trị của đạo hàm của hàm số mũ cơ số }\\
&\footnotesize\text{e cũng chính bằng hàm số đó: }\frac{d}{dt}e^t=e^t.\\
&\footnotesize\bull\text{Số e là số thực dương duy nhất mà } \frac{d}{dt}log_et=\frac{1}{t}.\\
&\footnotesize\bull\text{Số e là giới hạn của }(1 + \frac{1}{n})^n \text{ khi n tiến về vô cực là }e = \lim\limits_{n \to \infin}(1 + \frac{1}{n})^n.\\
&\footnotesize\bull\text{Số e cũng là tổng của chuỗi vô hạn trong đó n! là giai thừa của n: }\\
&\footnotesize\sum^e_{n=0}\frac{1}{n!}=\frac{1}{0!}+\frac{1}{1!}+ \frac{1}{2!}+\frac{1}{3!}+...\\
&\footnotesize\bull\text{Số e là số thực dương duy nhất mà }\int_1^e\frac{1}{t}dt=1. \text{ Nghĩa là diện tích hình }\\
&\footnotesize\text{phẳng được giới hạn bởi đồ thị hàm số }y=\frac{1}{t} \text{từ t = 1 đến t = e sẽ có diện }\\
&\footnotesize\text{tích bằng 1.}
\end{aligned}Để tính được nguyên hàm e mũ u, các em có thể áp dụng một số công thức thông qua các bảng nguyên hàm e mũ u cơ bản và kết hợp như sau:
\begin{aligned}
\hline
\begin{array}{|cc|}
&1. \int e^xdx=e^x+C\\ \hline
&2. \int e^udu=e^u+C \\ \hline
&3. \int e^{ax+b}dx=e^{ax+b}+C \\ \hline
&4. \int e^{-x}dx=-e^{-x}+C \\ \hline
&5. \int e^{-u}dx=-e^{-u}+C \\ \hline
\end{array}
\end{aligned}\def\arraystretch{1.5}
\begin{aligned}
\hline
\begin{array}{|cc|}
&6. \int cos(ax).e^{bx}=\frac{(asin(ax)+bcos(ax)).e^{bx}}{a^2+b^2}+C\\ \hline
&7. \int cos(au).e^{bu}=\frac{(bsin(au)-acos(au)).e^{bu}}{a^2+b^2}+C\\ \hline
&8. \int e^{au}du=\frac{e^{au}}{a}+C \\ \hline
&9. \int u.e^{au}du=(\frac{u}{a}-\frac{1}{a^2})e^{au}+C \\ \hline
&10. \int u^ne^{au}du=\frac{u^ne^{au}}{a}-\frac{n}{a} \int u^{n-1}e^{au}du+C
\\\hline
\end{array}
\end{aligned}Nguyên hàm e mũ u là phần kiến thức quan trọng của chương trình Toán đại số 12. Các em có thể học cùng bạn bè hoặc học online livestream qua nền tảng Marathon Education để củng cố kiến thức của mình.
Giáo viên tại Marathon đều thuộc TOP 1% các giáo viên dạy giỏi toàn quốc. Do đó, các em có thể yên tâm tiếp thu những kiến thức mà thầy cô truyền tải. Trong quá trình học tập, các em còn được hỗ trợ bởi đội ngũ cố vấn học tập chuyên môn.
Các yếu tố đường truyền, âm thanh hay hình ảnh luôn được đảm bảo thật rõ ràng và sắc nét. Có như vậy, việc học tập của các em mới không bị gián đoạn. Đồng thời, để giúp tạo ra sự kết nối giữa các em với thầy cô, các lớp học online tại Marathon còn được mô phỏng như một lớp học offline bình thường.
Ngoài lớp Toán, Marathon Education còn mở các lớp cho 2 môn tự nhiên khác là Lý và Hóa. Các em sẽ nhận ngay sổ tay học tập Toán – Lý – Hóa được biên soạn tỉ mỉ khi đăng ký lớp học. Điều này sẽ hỗ trợ các em trong quá trình ôn luyện và củng cố lại kiến thức tốt hơn.
Nếu có nhu cầu tham gia học tập, các em hãy nhanh tay đăng ký học online livestream Toán – Lý – Hóa ngay ngày hôm nay, trước 15/02/2022 để có cơ hội rinh ngay được nhiều ưu đãi hấp dẫn. Trên đây là các thông tin liên quan đến nguyên hàm e mũ u và các hàm số đơn giản. Hy vọng qua bài viết này, các em sẽ “bỏ túi” được nhiều kiến thức bổ ích và mới mẻ. Chúc các em có những giây phút học tập tràn đầy năng lượng và hiệu quả!